Fernique's theorem
In mathematics — specifically, in measure theory — Fernique's theorem is a result about Gaussian measures on Banach spaces. It extends the finite-dimensional result that a Gaussian random variable has exponential tails. The result was proved in 1970 by the mathematician Xavier Fernique.
Statement of the theorem
Let (X, || ||) be a separable Banach space. Let μ be a centered Gaussian measure on X, i.e. a probability measure defined on the Borel sets of X such that, for every bounded linear functional ℓ : X → R, the push-forward measure ℓ∗μ defined on the Borel sets of R by
is a Gaussian measure (a normal distribution) with zero mean. Then there exists α > 0 such that
A fortiori, μ (equivalently, any X-valued random variable G whose law is μ) has moments of all orders: for all k ≥ 0,
References
- Fernique, Xavier (1970). "Intégrabilité des vecteurs gaussiens". C. R. Acad. Sci. Paris Sér. A-B 270: A1698–A1699. MR0266263
- Giuseppe Da Prato and Jerzy Zabczyk, Stochastic equations in infinite dimension, Cambridge University Press, 1992. Theorem 2.6
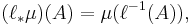
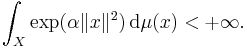
![\mathbb{E} [ \| G \|^{k} ] = \int_{X} \| x \|^{k} \, \mathrm{d} \mu (x) < %2B \infty.](/2012-wikipedia_en_all_nopic_01_2012/I/ecdaf238223f208ea405e479a1c884df.png)